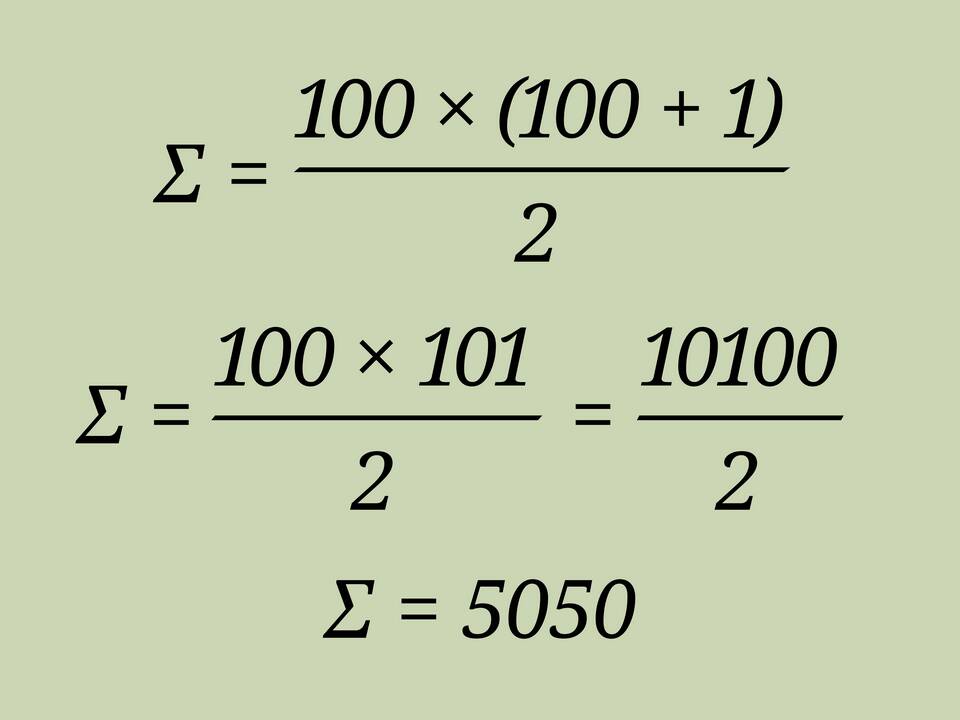- Математическое определение - результат операции сложения
- Обозначение - знак "+" между слагаемыми
- Компоненты - числа, которые складываются, называются слагаемыми
| Свойство | Формулировка | Пример |
| Коммутативность | От перемены мест слагаемых сумма не меняется | 2 + 3 = 3 + 2 |
| Ассоциативность | Группировка слагаемых не влияет на результат | (2 + 3) + 4 = 2 + (3 + 4) |
| Существование нуля | При сложении с нулем число не изменяется | 5 + 0 = 5 |
- Конечная сумма - сложение конечного числа слагаемых
- Бесконечный ряд - сумма бесконечного числа слагаемых
- Алгебраическая сумма - сумма, включающая положительные и отрицательные числа
- Векторная сумма - сложение векторов по правилам векторной алгебры
| Тип суммы | Пример | Результат |
| Простые числа | 7 + 8 | 15 |
| Десятичные дроби | 3.14 + 2.86 | 6.00 |
| Алгебраическая сумма | 5 + (-3) | 2 |
- В арифметике - базовые вычисления
- В алгебре - решение уравнений
- В геометрии - вычисление периметров
- В экономике - подсчет доходов и расходов
- В статистике - расчет суммарных показателей
| Система счисления | Пример | Результат |
| Двоичная | 101 + 110 | 1011 |
| Восьмеричная | 7 + 5 | 14 |
| Шестнадцатеричная | A + B | 15 |
Заключение
Сумма чисел является одной из основных операций в математике, имеющей широкое применение в различных областях знаний. Понимание свойств и особенностей сложения чисел позволяет эффективно решать как простейшие арифметические задачи, так и сложные математические проблемы. Освоение этого понятия составляет фундамент для дальнейшего изучения математики и ее приложений.