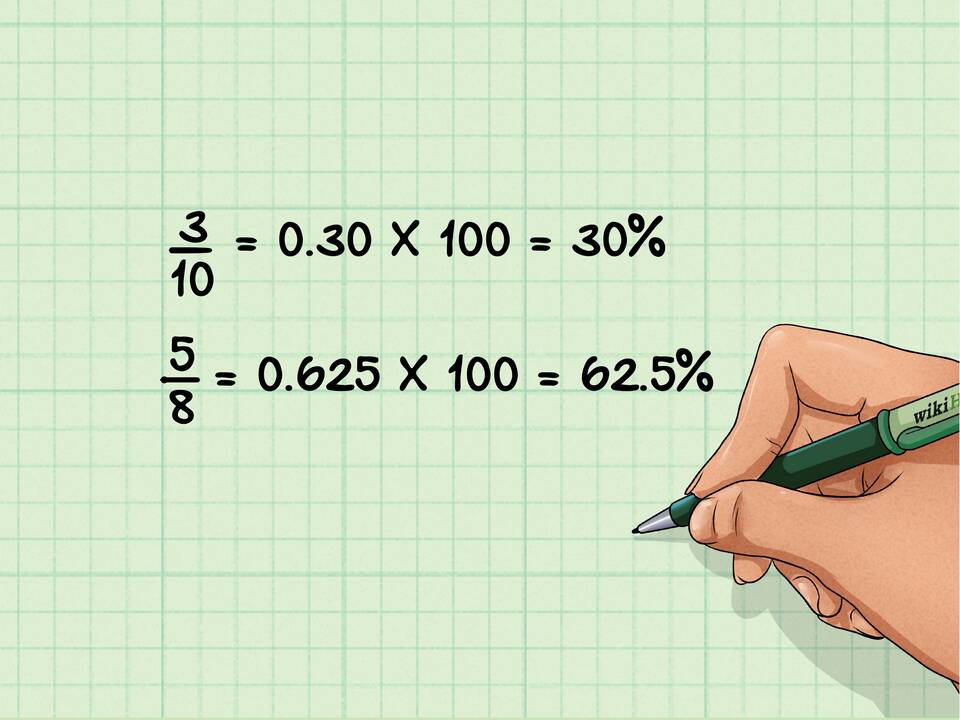Процент представляет собой сотую часть целого. Для перевода любого значения в проценты необходимо выполнить простое математическое преобразование.
Содержание
Базовые принципы перевода в проценты
Основные методы преобразования
Перевод десятичной дроби в проценты
- Возьмите десятичную дробь (например, 0.75)
- Умножьте ее на 100 (0.75 × 100 = 75)
- Добавьте знак процента (75%)
Перевод обыкновенной дроби в проценты
- Разделите числитель на знаменатель (3/4 = 0.75)
- Умножьте результат на 100 (0.75 × 100 = 75)
- Получите процентное значение (75%)
Практические примеры преобразования
| Исходное значение | Действие | Результат |
| 0.25 | 0.25 × 100 | 25% |
| 1/2 | (1 ÷ 2) × 100 | 50% |
| 0.8 | 0.8 × 100 | 80% |
| 3/5 | (3 ÷ 5) × 100 | 60% |
Специальные случаи преобразования
Перевод целых чисел в проценты
- Целое число равно 100% (5 = 500%)
- Для части от целого: (часть ÷ целое) × 100
Обратный перевод процентов в десятичные дроби
- Уберите знак процента (75% → 75)
- Разделите на 100 (75 ÷ 100 = 0.75)
Применение в программах
В Microsoft Excel
- Выделите ячейки с числами
- Нажмите кнопку "%" на панели инструментов
- Или умножьте значение на 100 вручную
В языках программирования
| Язык | Пример кода |
| Python | percent = value * 100 |
| JavaScript | let percent = value * 100; |
Проверка правильности расчетов
Для проверки преобразования:
- 100% должно соответствовать единице (1)
- 50% должно равняться 0.5
- Сумма процентов частей должна давать 100%